NN-Z2H Lesson 5: Building makemore part 4 - Becoming a Backprop Ninja

This is not orginal content!

This is my study notes / codes along with Andrej Karpathy’s “Neural Networks: Zero to Hero” series.

intro: why you should care

swole doge style backpropagation, image credit to this video

In the previous lecture, we’re introduced to some common issues with our “shallow” (and of course for deep as well) neural network and how to fix with the initialization setting and Batch Normalization. We’re also learned some diagnostic tools to observe forward pass activations, backward pass gradients, and weights update, to calibrate the training loop. In this lecture, we aim to replace this line of code:

... loss.backward() ...

with from-scratch-code. It’s basically identical to MicroGrad, but on Tensor rather than Scalar. But why we should care?

The problem with Backpropagation is that it is a leaky abstraction. – Andrej Karpathy

readmore: - https://karpathy.medium.com/yes-you-should-understand-backprop-e2f06eab496b, - and https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html.

inshort, to effectively debug neural network, we should be deeply understanding how back propagation work under the hood. Let’s do it!

starter code

import libraries:

import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline

read data:

import pandas as pd

url = "https://raw.githubusercontent.com/karpathy/makemore/refs/heads/master/names.txt"
words = pd.read_csv(url, header=None).iloc[:, 0].tolist()
words[:8]

['emma', 'olivia', 'ava', 'isabella', 'sophia', 'charlotte', 'mia', 'amelia']

build vocab:

# build the vocabulary of characters and mapping to/from integer
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i, s in enumerate(chars)}
stoi['.'] = 0
itos = {i: s for s, i in stoi.items()}
vocab_size = len(itos)
print(itos)
print(vocab_size)

{1: 'a', 2: 'b', 3: 'c', 4: 'd', 5: 'e', 6: 'f', 7: 'g', 8: 'h', 9: 'i', 10: 'j', 11: 'k', 12: 'l', 13: 'm', 14: 'n', 15: 'o', 16: 'p', 17: 'q', 18: 'r', 19: 's', 20: 't', 21: 'u', 22: 'v', 23: 'w', 24: 'x', 25: 'y', 26: 'z', 0: '.'}
27

build dataset splits (identical to previous so I folded it):

block_size = 3 # context length: how many characters do we take to predict the next one.
# build the dataset
def buid_dataset(words):
    X, Y = [], []

    for w in words:
        context = [0] * block_size
        for ch in w + '.':
            ix = stoi[ch]
            X.append(context)
            Y.append(ix)
            context = context[1:] + [ix]

    X = torch.tensor(X)
    Y = torch.tensor(Y)
    print(X.shape, Y.shape)
    return X, Y

import random
random.seed(42)
random.shuffle(words)
n1 = int(0.8 * len(words))
n2 = int(0.9 * len(words))

Xtr, Ytr = buid_dataset(words[:n1])        # 80#
Xdev, Ydev = buid_dataset(words[n1:n2])    # 10%
Xte, Yte = buid_dataset(words[n2:])        # 10%

torch.Size([182625, 3]) torch.Size([182625])
torch.Size([22655, 3]) torch.Size([22655])
torch.Size([22866, 3]) torch.Size([22866])

utility function we will use later when comparing manual gradients to PyTorch gradients.

def cmp(s, dt, t):
  ex = torch.all(dt == t.grad).item()
  app = torch.allclose(dt, t.grad)
  maxdiff = (dt - t.grad).abs().max().item()
  print(f'{s:15s} | exact: {str(ex):5s} | approximate: {str(app):5s} | maxdiff: {maxdiff}')

network construction:

n_embd = 10 # the dimensionality of the character embedding vectors
n_hidden = 64 # the number of neurons in the hidden layer of the MLP

g = torch.Generator().manual_seed(2147483647) # for reproducibility
C  = torch.randn((vocab_size, n_embd),            generator=g)
# Layer 1
W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * (5/3)/((n_embd * block_size)**0.5)
b1 = torch.randn(n_hidden,                        generator=g) * 0.1 # using b1 just for fun, it's useless because of BN
# Layer 2
W2 = torch.randn((n_hidden, vocab_size),          generator=g) * 0.1
b2 = torch.randn(vocab_size,                      generator=g) * 0.1
# BatchNorm parameters
bngain = torch.randn((1, n_hidden))*0.1 + 1.0
bnbias = torch.randn((1, n_hidden))*0.1

# Note: I am initializating many of these parameters in non-standard ways
# because sometimes initializating with e.g. all zeros could mask an incorrect
# implementation of the backward pass.

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
print(sum(p.nelement() for p in parameters)) # number of parameters in total
for p in parameters:
  p.requires_grad = True

4137

mini-batch construction:

batch_size = 32
n = batch_size # a shorter variable also, for convenience
# construct a minibatch
ix = torch.randint(0, Xtr.shape[0], (batch_size,), generator=g)
Xb, Yb = Xtr[ix], Ytr[ix] # batch X,Y

forward pass, “chunkated” into smaller steps that are possible to backward one at a time.

emb = C[Xb] # embed the characters into vectors
embcat = emb.view(emb.shape[0], -1) # concatenate the vectors

# Linear layer 1
hprebn = embcat @ W1 + b1 # hidden layer pre-activation

# BatchNorm layer
bnmeani = 1/n*hprebn.sum(0, keepdim=True)
bndiff = hprebn - bnmeani
bndiff2 = bndiff**2
bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # note: Bessel's correction (dividing by n-1, not n)
bnvar_inv = (bnvar + 1e-5)**-0.5
bnraw = bndiff * bnvar_inv
hpreact = bngain * bnraw + bnbias

# Non-linearity
h = torch.tanh(hpreact) # hidden layer

# Linear layer 2
logits = h @ W2 + b2 # output layer

# cross entropy loss (same as F.cross_entropy(logits, Yb)), Kullback–Leibler divergence
logit_maxes = logits.max(1, keepdim=True).values
norm_logits = logits - logit_maxes # subtract max for numerical stability
counts = norm_logits.exp()
counts_sum = counts.sum(1, keepdims=True)
counts_sum_inv = counts_sum**-1 # if I use (1.0 / counts_sum) instead then I can't get backprop to be bit exact...
probs = counts * counts_sum_inv
logprobs = probs.log()
loss = -logprobs[range(n), Yb].mean()

# PyTorch backward pass
for p in parameters:
  p.grad = None
for t in [logprobs, probs, counts, counts_sum, counts_sum_inv, # afaik there is no cleaner way
          norm_logits, logit_maxes, logits, h, hpreact, bnraw,
         bnvar_inv, bnvar, bndiff2, bndiff, hprebn, bnmeani,
         embcat, emb]:
  t.retain_grad()

hprebn.retain_grad() # Tuan added this line since code above does not ensure hprebn's grad to be retained.

loss.backward()
loss

tensor(3.3267, grad_fn=<NegBackward0>)

exercise 1: backproping the atomic compute graph

I can do 60, 70% of this myself ~ for popular mathematics operations. What I need to remember after these excercises are backwards of:

• elements in matrix mult;
• max operator;
• indexing operator; and
• broadcasting behavior.

Andrej inductive reasoning, explains how to get a derivative from matrix multiplication.

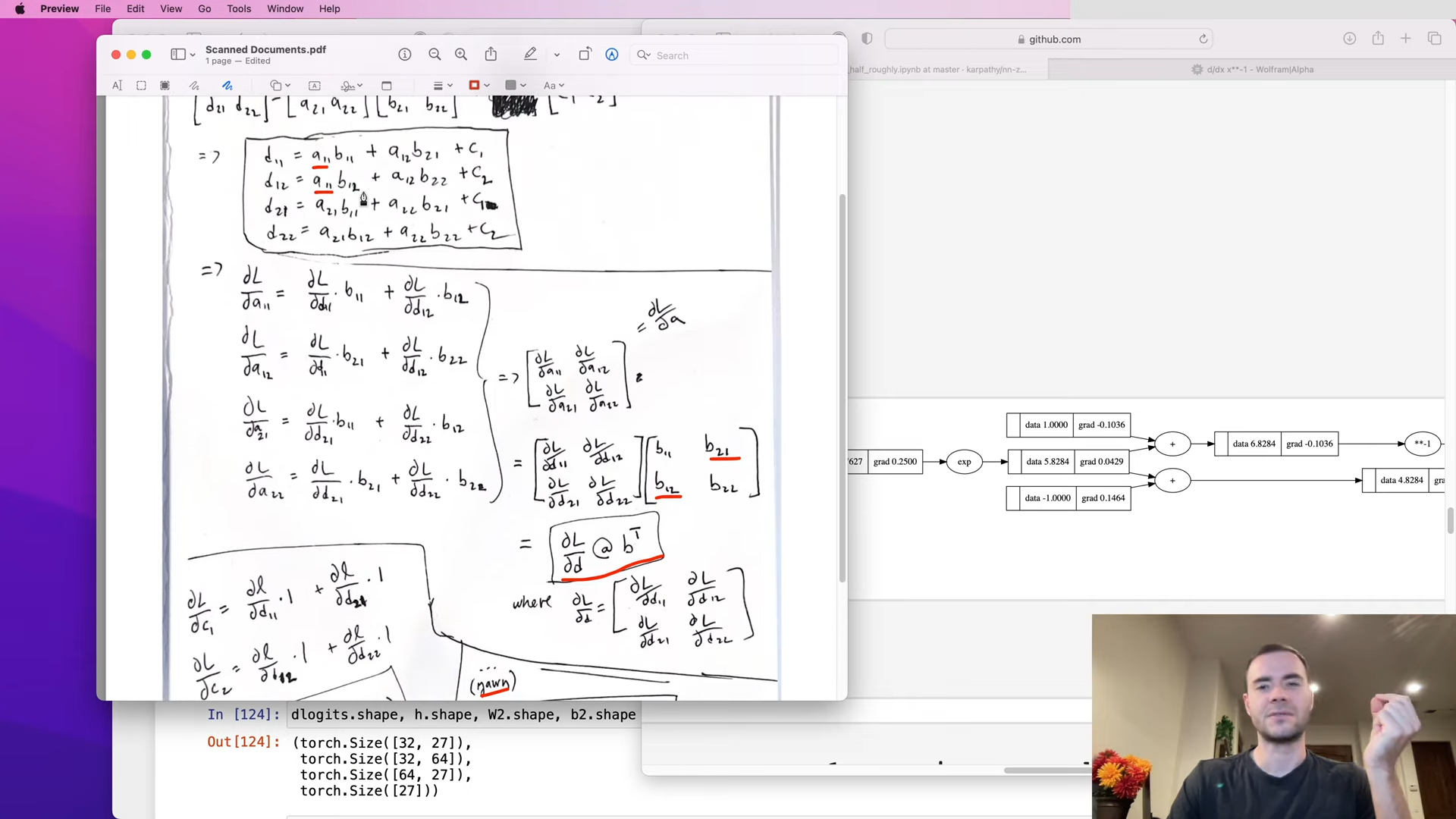
Given the matrix mult expression \(d = a @ b + c\), we have:

• \(\frac{\partial L}{\partial \mathbf{a}} = \frac{\partial L}{\partial \mathbf{d}} @ \mathbf{b}^T\)
• \(\frac{\partial L}{\partial \mathbf{b}} = \mathbf{a}^T @ \frac{\partial L}{\partial \mathbf{d}}\)
• \(\frac{\partial L}{\partial \mathbf{c}} = \frac{\partial L}{\partial \mathbf{d}}.sum(0)\)

# Exercise 1: backprop through the whole thing manually, 
# backpropagating through exactly all of the variables 
# as they are defined in the forward pass above, one by one
print("Cross entropy loss".upper())
dlogprobs = torch.zeros_like(logprobs) # create zeros tensor with same size
dlogprobs[range(n), Yb] = - 1.0 / n
dprobs = torch.zeros_like(probs) 
dprobs = (1.0 / probs) * dlogprobs
dcounts_sum_inv = (counts * dprobs).sum(1, keepdim=True)
dcounts_sum = (-1 * counts_sum**-2) * dcounts_sum_inv
dcounts = torch.ones_like(counts) * dcounts_sum + counts_sum_inv * dprobs
dnorm_logits = (norm_logits.exp()) * dcounts # = counts * dcounts
dlogit_maxes = (- dnorm_logits).sum(1, keepdim=True) # broadcasting, again

cmp('logprobs', dlogprobs, logprobs)
cmp('probs', dprobs, probs)
cmp('counts_sum_inv', dcounts_sum_inv, counts_sum_inv)
cmp('counts_sum', dcounts_sum, counts_sum)
cmp('counts', dcounts, counts)
cmp('norm_logits', dnorm_logits, norm_logits)
cmp('logit_maxes', dlogit_maxes, logit_maxes)


dlogits = (dnorm_logits.clone() 
          + F.one_hot( logits.max(1).indices, # broadcasting, again
                        num_classes=logits.shape[1]
                        ) * dlogit_maxes)

print("Layer 2 with Linear and Non-linearity tanh".upper())
dh =  dlogits @ W2.T
dW2 = h.T @ dlogits
db2 = dlogits.sum(0) # sum by column, vertical, to eliminate the 0-index dim

cmp('logits', dlogits, logits)
cmp('h', dh, h)
cmp('W2', dW2, W2)
cmp('b2', db2, b2)

print("Batch Norm layer".upper())
dhpreact = (1 - h**2) * dh # output of the tanh, square
dbngain = (bnraw * dhpreact).sum(0, keepdim=True)
dbnbias = dhpreact.sum(0, keepdim=True)
dbnraw = bngain * dhpreact
dbnvar_inv = (bndiff * dbnraw).sum(0, keepdim=True)
dbnvar = (-0.5 * (bnvar + 1e-5)**-1.5) * dbnvar_inv
dbndiff2 = 1/(n-1) * torch.ones_like(bndiff2) * dbnvar
dbndiff = bnvar_inv * dbnraw + 2 * bndiff * dbndiff2
dbnmeani = (- torch.ones_like(dbndiff) * dbndiff).sum(0)

cmp('hpreact', dhpreact, hpreact)
cmp('bngain', dbngain, bngain)
cmp('bnbias', dbnbias, bnbias)
cmp('bnraw', dbnraw, bnraw)
cmp('bnvar_inv', dbnvar_inv, bnvar_inv)
cmp('bnvar', dbnvar, bnvar)
cmp('bndiff2', dbndiff2, bndiff2)
cmp('bndiff', dbndiff, bndiff)
cmp('bnmeani', dbnmeani, bnmeani)

print("Linear layer 1".upper())
dhprebn = dbndiff.clone() + (1.0/n * (torch.ones_like(hprebn) * dbnmeani))
dembcat = dhprebn @ W1.T
dW1 = embcat.T @ dhprebn
db1 = dhprebn.sum(0, keepdim=True)
demb = dembcat.view(emb.shape)
dC = torch.zeros_like(C)
for k in range(Xb.shape[0]): # iterate all elements of the Xb
  for j in range(Xb.shape[1]):
    ix = Xb[k,j]
    dC[ix] += demb[k,j]
# Method 2
dC = torch.zeros_like(C)
dC.index_add_(0, Xb.view(-1), demb.view(-1, 10))

cmp('hprebn', dhprebn, hprebn)
cmp('embcat', dembcat, embcat)
cmp('W1', dW1, W1)
cmp('b1', db1, b1)
cmp('emb', demb, emb)
cmp('C', dC, C)

1

dlogprobs: logprobs is an (32, 27) array - contains log probabilities of every character in 27 vocab for 32 output. loss just indexes ((range(n), Yb)) to pick out the corresponding numbers of the ground trues, then do mean (1 / n) and get negative (-). So the grad for each element that had been picked out is -1/n, while for others is 0;

2

dprobs: d/dx log(x) is just 1/x - local derivative, then multiply by next leaf grad dlogprobs, element wise;

3

dcounts_sum_inv: should be counts * dprobs according to chainrule. But remember counts.shape is (32, 27), and counts_sum_inv.shape is (32, 1), then there is broadcasting to 27 columns. counts_sum_inv is being used multiple times in the topo/diagram -> we need to sum them (grad) up. We do it by columns so Keepdim=True;

4

dcount: was used in 2 expression, so it would be the sum of (1) counts_sum_inv * dprobs - same with dcounts_sum_inv by symmetry, and (2) torch.ones_like(counts) * dcounts_sum - the gradient flow from dcounts_sum equally, and equal to 1;

5

dlogits: sum of 2 flows, the 2nd one for max() operations -> gradient should be the 1 for those max elements, the remain would be 0;

6

Notice the vertical broadcasting of bngain and bnbias;

7

Need to sum up vertically because bnvar_inv is (1, 64) while 2 multipliers are (32, 64);

8

Undo the concatenation;

9

Undo the indexing: emb.shape = (32, 3, 10), C.shape = (27, 10), Xb.shape = (32, 3).

CROSS ENTROPY LOSS
logprobs        | exact: True  | approximate: True  | maxdiff: 0.0
probs           | exact: True  | approximate: True  | maxdiff: 0.0
counts_sum_inv  | exact: True  | approximate: True  | maxdiff: 0.0
counts_sum      | exact: True  | approximate: True  | maxdiff: 0.0
counts          | exact: True  | approximate: True  | maxdiff: 0.0
norm_logits     | exact: True  | approximate: True  | maxdiff: 0.0
logit_maxes     | exact: True  | approximate: True  | maxdiff: 0.0
LAYER 2 WITH LINEAR AND NON-LINEARITY TANH
logits          | exact: True  | approximate: True  | maxdiff: 0.0
h               | exact: True  | approximate: True  | maxdiff: 0.0
W2              | exact: True  | approximate: True  | maxdiff: 0.0
b2              | exact: True  | approximate: True  | maxdiff: 0.0
BATCH NORM LAYER
hpreact         | exact: True  | approximate: True  | maxdiff: 0.0
bngain          | exact: True  | approximate: True  | maxdiff: 0.0
bnbias          | exact: True  | approximate: True  | maxdiff: 0.0
bnraw           | exact: True  | approximate: True  | maxdiff: 0.0
bnvar_inv       | exact: True  | approximate: True  | maxdiff: 0.0
bnvar           | exact: True  | approximate: True  | maxdiff: 0.0
bndiff2         | exact: True  | approximate: True  | maxdiff: 0.0
bndiff          | exact: True  | approximate: True  | maxdiff: 0.0
bnmeani         | exact: True  | approximate: True  | maxdiff: 0.0
LINEAR LAYER 1
hprebn          | exact: True  | approximate: True  | maxdiff: 0.0
embcat          | exact: True  | approximate: True  | maxdiff: 0.0
W1              | exact: True  | approximate: True  | maxdiff: 0.0
b1              | exact: True  | approximate: True  | maxdiff: 0.0
emb             | exact: True  | approximate: True  | maxdiff: 0.0
C               | exact: True  | approximate: True  | maxdiff: 0.0

brief digression: bessel’s correction in batchnorm

The paper of Batch Norm inconsistantly mentioned that:

• they used biased variance for training;
• and used un-biased variance for inference.

We train on small mini-batch, so should be using un-biased variance. PyTorch, since implemented what exactly paper wrote, has this discrepancy.

exercise 2: cross entropy loss backward pass

We are realizing that we doing too much work since we need to break the loss calculation from logits into too many steps that (1) they are easy enough for us to do backpropagation, but (2) most of them can cancel each other out. So in exercise two, we need to convert those bunch of atomic pieces of calculation to a shorter formula of cross entropy that can facilitate the backpropating.

# Exercise 2: backprop through cross_entropy but all in one go
# to complete this challenge look at the mathematical expression of the loss,
# take the derivative, simplify the expression, and just write it out

# forward pass

# before:
# logit_maxes = logits.max(1, keepdim=True).values
# norm_logits = logits - logit_maxes # subtract max for numerical stability
# counts = norm_logits.exp()
# counts_sum = counts.sum(1, keepdims=True)
# counts_sum_inv = counts_sum**-1 # if I use (1.0 / counts_sum) instead then I can't get backprop to be bit exact...
# probs = counts * counts_sum_inv
# logprobs = probs.log()
# loss = -logprobs[range(n), Yb].mean()

# now:
loss_fast = F.cross_entropy(logits, Yb)
print(loss_fast.item(), 'diff:', (loss_fast - loss).item())

3.3267292976379395 diff: 4.76837158203125e-07

Mathematically given the Cross-Entropy loss formula:

\(L = -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{k} Y_{ij} \log(\hat{Y}_{ij})\)

with \(\hat{Y}{ij}\) is calculated by the softmax transformation:

\(\hat{Y}{ij} = \frac{\exp(\text{logits}{ij})}{\sum_{c=1}^{k} \exp(\text{logits}_{ic})}\)

where:

• \(n\): batch size, in this case is 32 - n;
• \(k\): vocab size or number of classes, in this case is 27 - vocab_size;
• \(Y \in {0,1}^{n \times k}\): one-hot encoding maxtrix (ground truth) - Y;
• \(\text{logits} \in \mathbb{R}^{n \times k}\): raw logits, input of softmax layer - logits;
• \(\hat{Y} \in [0,1]^{n \times k}\): probabilities after softmax layer - probs.

I actually can not do this exercise so AK’s solution here:

# backward pass

dlogits = F.softmax(logits, 1)
dlogits[range(n), Yb] -= 1.0
dlogits *= n**-1.0

cmp('logits', dlogits, logits) # I can only get approximate to be true, my maxdiff is 6e-9

logits          | exact: False | approximate: True  | maxdiff: 6.752088665962219e-09

I will comeback with another post on thisss: the backward for cross entropy loss.

what is dlogits intuitively?

Now let’s look how dlogits look like.

This is the first row of logits through softmax layer, it’s probabilities of every possible character in vocab size 27, they are all small and sum of them is 1.

F.softmax(logits, 1)[0]

tensor([0.0765, 0.0852, 0.0175, 0.0537, 0.0181, 0.0835, 0.0274, 0.0357, 0.0181,
        0.0319, 0.0393, 0.0355, 0.0382, 0.0277, 0.0341, 0.0135, 0.0096, 0.0207,
        0.0163, 0.0540, 0.0484, 0.0206, 0.0263, 0.0672, 0.0549, 0.0257, 0.0205],
       grad_fn=<SelectBackward0>)

And this is the first row of dlogits multiplied by n for comparision, it’s all identical excep the 8th probability (Xb[0] = 8). And sum of them is 0!

dlogits[0] * n

tensor([ 0.0765,  0.0852,  0.0175,  0.0537,  0.0181,  0.0835,  0.0274,  0.0357,
        -0.9819,  0.0319,  0.0393,  0.0355,  0.0382,  0.0277,  0.0341,  0.0135,
         0.0096,  0.0207,  0.0163,  0.0540,  0.0484,  0.0206,  0.0263,  0.0672,
         0.0549,  0.0257,  0.0205], grad_fn=<MulBackward0>)

So for each data point in the batch of 32, we pushnish super hard the correct character, making the magnitude of it’s grad is so high (negative number), then the prob of that predict-character can change toward to correct one. This push and pull is somehow the way that network learn.

plt.figure(figsize=(8, 8))
plt.imshow(dlogits.detach(), cmap="gray")

When the network perfectly predict, softmax will have a full row vector except the 8th prob, which is 1. Then the dlogits will be full of 0, the network stop learning.

exercise 3: batch norm layer backward pass

# Exercise 3: backprop through batchnorm but all in one go
# to complete this challenge look at the mathematical expression of the output of batchnorm,
# take the derivative w.r.t. its input, simplify the expression, and just write it out

# forward pass

# before:
# bnmeani = 1/n*hprebn.sum(0, keepdim=True)
# bndiff = hprebn - bnmeani
# bndiff2 = bndiff**2
# bnvar = 1/(n-1)*(bndiff2).sum(0, keepdim=True) # note: Bessel's correction (dividing by n-1, not n)
# bnvar_inv = (bnvar + 1e-5)**-0.5
# bnraw = bndiff * bnvar_inv
# hpreact = bngain * bnraw + bnbias

# now:
hpreact_fast = bngain * (hprebn - hprebn.mean(0, keepdim=True)) / torch.sqrt(hprebn.var(0, keepdim=True, unbiased=True) + 1e-5) + bnbias
print('max diff:', (hpreact_fast - hpreact).abs().max())

max diff: tensor(4.7684e-07, grad_fn=<MaxBackward1>)

Below is the image of Batch Norm algorithm:

Batch Normalization algo, source

And this is flowchart

flowchart LR

Input(...) --> X(x)
X(x) -- "(4) dL/dx" --> Mu(mu)
X(x) -- "(4) dL/dx" --> Si("sigma (square)")
X(x) -- "(4) dL/dx" --> Xh(x_hat)
Si("sigma (square)") -- "(2) dL/dsigma" --> Xh(x_hat)
Mu(mu) -- "(3.1) dL/dmu" --> Xh(x_hat)
Mu(mu) -- "(3.2) dL/dmu" --> Si("sigma (square)")
Xh(x_hat) -- "(1) dL/dx_hat" --> Y(y)

G(gamma) --> Y(y)
B(beta) --> Y(y)

We will need to calculate dL/dx given dL/dy, we will calculate by hand reversely:

1. scale and shift: dL/dx_hat = gamma * dL/dy easy enough;
2. normalize: dL/dsigma = -1/2 * gamma * SUM[dL/dy * (x - mu) * (sigma^2 + eps)^(-3/2)];
3. normalize & mini-batch variance: dL/dmu = - SUM[dL/dy * gamma * (sigma^2 + eps)^(-1/2)], this is path (3.1), we can prove that path (3.2) equal to zero - since mu is average of x, we can think of change in mu will be eliminated by x itself w.r.t. L;
4. given all the gradients above, we just write the expressions down and do some transformation, this is the final: dL/dx = gamma * (sigma^2 + eps)^(-1/2) / m { [m * dL/dy] - SUMj[dL/dy] - m/(m-1) * x_hat * SUMj[dL/dy * x_hat]}, where m is mini-batch size (in our data is n)

# backward pass

# before we had:
# dbnraw = bngain * dhpreact
# dbndiff = bnvar_inv * dbnraw
# dbnvar_inv = (bndiff * dbnraw).sum(0, keepdim=True)
# dbnvar = (-0.5*(bnvar + 1e-5)**-1.5) * dbnvar_inv
# dbndiff2 = (1.0/(n-1))*torch.ones_like(bndiff2) * dbnvar
# dbndiff += (2*bndiff) * dbndiff2
# dhprebn = dbndiff.clone()
# dbnmeani = (-dbndiff).sum(0)
# dhprebn += 1.0/n * (torch.ones_like(hprebn) * dbnmeani)

# calculate dhprebn given dhpreact (i.e. backprop through the batchnorm)
# (you'll also need to use some of the variables from the forward pass up above)

dhprebn = bngain * bnvar_inv / n * ( n * dhpreact - dhpreact.sum(0)  - n / (n-1) * bnraw * (dhpreact * bnraw).sum(0))

cmp('hprebn', dhprebn, hprebn) # I can only get approximate to be true, my maxdiff is 9e-10

hprebn          | exact: False | approximate: True  | maxdiff: 9.313225746154785e-10

exercise 4: putting it all together

# Exercise 4: putting it all together!
# Train the MLP neural net with your own backward pass

# init
n_embd = 10 # the dimensionality of the character embedding vectors
n_hidden = 200 # the number of neurons in the hidden layer of the MLP

g = torch.Generator().manual_seed(2147483647) # for reproducibility
C  = torch.randn((vocab_size, n_embd),            generator=g)
# Layer 1
W1 = torch.randn((n_embd * block_size, n_hidden), generator=g) * (5/3)/((n_embd * block_size)**0.5)
b1 = torch.randn(n_hidden,                        generator=g) * 0.1
# Layer 2
W2 = torch.randn((n_hidden, vocab_size),          generator=g) * 0.1
b2 = torch.randn(vocab_size,                      generator=g) * 0.1
# BatchNorm parameters
bngain = torch.randn((1, n_hidden))*0.1 + 1.0
bnbias = torch.randn((1, n_hidden))*0.1

parameters = [C, W1, b1, W2, b2, bngain, bnbias]
print(sum(p.nelement() for p in parameters)) # number of parameters in total
for p in parameters:
  p.requires_grad = True

# same optimization as last time
max_steps = 200000
batch_size = 32
n = batch_size # convenience
lossi = []

# use this context manager for efficiency once your backward pass is written (TODO)
with torch.no_grad():

  # kick off optimization
  for i in range(max_steps):

    # minibatch construct
    ix = torch.randint(0, Xtr.shape[0], (batch_size,), generator=g)
    Xb, Yb = Xtr[ix], Ytr[ix] # batch X,Y

    # forward pass
    emb = C[Xb] # embed the characters into vectors
    embcat = emb.view(emb.shape[0], -1) # concatenate the vectors
    # Linear layer
    hprebn = embcat @ W1 + b1 # hidden layer pre-activation
    # BatchNorm layer
    # -------------------------------------------------------------
    bnmean = hprebn.mean(0, keepdim=True)
    bnvar = hprebn.var(0, keepdim=True, unbiased=True)
    bnvar_inv = (bnvar + 1e-5)**-0.5
    bnraw = (hprebn - bnmean) * bnvar_inv
    hpreact = bngain * bnraw + bnbias
    # -------------------------------------------------------------
    # Non-linearity
    h = torch.tanh(hpreact) # hidden layer
    logits = h @ W2 + b2 # output layer
    loss = F.cross_entropy(logits, Yb) # loss function

    # backward pass
    for p in parameters:
      p.grad = None
    # loss.backward() # use this for correctness comparisons, delete it later!

    # manual backprop! #swole_doge_meme
    # -----------------
    dlogits = F.softmax(logits, 1)
    dlogits[range(n), Yb] -= 1
    dlogits /= n
    # 2nd layer backprop
    dh = dlogits @ W2.T
    dW2 = h.T @ dlogits
    db2 = dlogits.sum(0)
    # tanh
    dhpreact = (1.0 - h**2) * dh
    # batchnorm backprop
    dbngain = (bnraw * dhpreact).sum(0, keepdim=True)
    dbnbias = dhpreact.sum(0, keepdim=True)
    dhprebn = bngain*bnvar_inv/n * (n*dhpreact - dhpreact.sum(0) - n/(n-1)*bnraw*(dhpreact*bnraw).sum(0))
    # 1st layer
    dembcat = dhprebn @ W1.T
    dW1 = embcat.T @ dhprebn
    db1 = dhprebn.sum(0)
    # embedding
    demb = dembcat.view(emb.shape)
    dC = torch.zeros_like(C)
    for k in range(Xb.shape[0]):
      for j in range(Xb.shape[1]):
        ix = Xb[k,j]
        dC[ix] += demb[k,j]
    grads = [dC, dW1, db1, dW2, db2, dbngain, dbnbias]
    # -----------------

    # update
    lr = 0.1 if i < 100000 else 0.01 # step learning rate decay
    for p, grad in zip(parameters, grads):
      #p.data += -lr * p.grad # old way of cheems doge (using PyTorch grad from .backward())
      p.data += -lr * grad # new way of swole doge TODO: enable

    # track stats
    if i % 10000 == 0: # print every once in a while
      print(f'{i:7d}/{max_steps:7d}: {loss.item():.4f}')
    lossi.append(loss.log10().item())

    # if i >= 100: # TODO: delete early breaking when you're ready to train the full net
    #   break

12297
      0/ 200000: 3.8430
  10000/ 200000: 2.1560
  20000/ 200000: 2.4334
  30000/ 200000: 2.4665
  40000/ 200000: 1.9888
  50000/ 200000: 2.3378
  60000/ 200000: 2.4149
  70000/ 200000: 2.0440
  80000/ 200000: 2.3377
  90000/ 200000: 2.1847
 100000/ 200000: 1.9861
 110000/ 200000: 2.2556
 120000/ 200000: 2.0190
 130000/ 200000: 2.4322
 140000/ 200000: 2.3159
 150000/ 200000: 2.2161
 160000/ 200000: 1.8835
 170000/ 200000: 1.8359
 180000/ 200000: 2.0352
 190000/ 200000: 1.8955

We can check gradients using this:

# useful for checking your gradients
for p,g in zip(parameters, grads):
  # g.requires_grad = True
  # g.retain_grad()
  cmp(str(tuple(p.shape)), g, p)

Calibrate the batch norm at the end of training:

with torch.no_grad():
  # pass the training set through
  emb = C[Xtr]
  embcat = emb.view(emb.shape[0], -1)
  hpreact = embcat @ W1 + b1
  # measure the mean/std over the entire training set
  bnmean = hpreact.mean(0, keepdim=True)
  bnvar = hpreact.var(0, keepdim=True, unbiased=True)

Evaluate train and val loss:

@torch.no_grad() # this decorator disables gradient tracking
def split_loss(split):
  x,y = {
    'train': (Xtr, Ytr),
    'val': (Xdev, Ydev),
    'test': (Xte, Yte),
  }[split]
  emb = C[x] # (N, block_size, n_embd)
  embcat = emb.view(emb.shape[0], -1) # concat into (N, block_size * n_embd)
  hpreact = embcat @ W1 + b1
  hpreact = bngain * (hpreact - bnmean) * (bnvar + 1e-5)**-0.5 + bnbias
  h = torch.tanh(hpreact) # (N, n_hidden)
  logits = h @ W2 + b2 # (N, vocab_size)
  loss = F.cross_entropy(logits, y)
  print(split, loss.item())

split_loss('train')
split_loss('val')

train 2.0704638957977295
val 2.10821533203125

Similar to what we achieved before!

Sample from model:

# sample from the model
g = torch.Generator().manual_seed(2147483647 + 10)

for _ in range(20):
    
    out = []
    context = [0] * block_size # initialize with all ...
    while True:
      # ------------
      # forward pass:
      # Embedding
      emb = C[torch.tensor([context])] # (1,block_size,d)      
      embcat = emb.view(emb.shape[0], -1) # concat into (N, block_size * n_embd)
      hpreact = embcat @ W1 + b1
      hpreact = bngain * (hpreact - bnmean) * (bnvar + 1e-5)**-0.5 + bnbias
      h = torch.tanh(hpreact) # (N, n_hidden)
      logits = h @ W2 + b2 # (N, vocab_size)
      # ------------
      # Sample
      probs = F.softmax(logits, dim=1)
      ix = torch.multinomial(probs, num_samples=1, generator=g).item()
      context = context[1:] + [ix]
      out.append(ix)
      if ix == 0:
        break
    
    print(''.join(itos[i] for i in out))

mora.
mayah.
see.
madyn.
alayethruthadra.
gradelyn.
elin.
shi.
jenleigh.
sana.
arleigh.
malaia.
noshubergshira.
sten.
joselle.
jose.
casun.
macder.
yarulyeh.
yuma.

outro

We have gone through and learned how can we manually do the gradients in our networks, it’s just some line of code for each step and pretty simple (but not for the Batch Norm formula 😪). And I’ll also be back with another post to calculate how the grad of cross entropy is coming.

In next lesson we will build RNN, LSTM, GRU, etc. Interesting and happly leanring!

resources

1. Notebook: https://github.com/karpathy/nn-zero-to-hero/blob/master/lectures/makemore/makemore_part4_backprop.ipynb;
2. Colab notebook: https://colab.research.google.com/drive/1WV2oi2fh9XXyldh02wupFQX0wh5ZC-z-?usp=sharing