NN-Z2H Lesson 1: The spelled-out intro to neural networks and backpropagation - building micrograd

Upfront-note: There are also greate resources in Vietnamese for learning Backpropagation, for e.g.:

1. Blog machinelearningcoban
2. Blog dominhhai

MicroGrad from scratch Yayy!

🚀 MicroGrad repo 🔥 Video Lecture

Backpropagation in Neural Networks, photo credit to GeekforGeek

intro & micrograd overview - what does your neural network training look like under the hood?

What is MicroGrad ❓: a tiny auto-grad (automatic gradient) engine, implement of backpropagation ~ itertively tune the weight of that nn to minimize the loss function -> improve the accuracy of the neural network. Backpropagation will be the mathematical core of any modern deep neutral network like, say pytorch, or jaxx.

Installation: pip install micrograd

Example:

from micrograd.engine import Value

a = Value(-4.0)
b = Value(2.0)
c = a + b
d = a * b + b**3
c += c + 1
c += 1 + c + (-a)
d += d * 2 + (b + a).relu()
d += 3 * d + (b - a).relu()
e = c - d
f = e**2
g = f / 2.0
g += 10.0 / f
print(f'{g.data:.4f}') # prints 24.7041, the outcome of this forward pass
g.backward()
print(f'{a.grad:.4f}') # prints 138.8338, i.e. the numerical value of dg/da
print(f'{b.grad:.4f}') # prints 645.5773, i.e. the numerical value of dg/db

1

Micrograd allows you to build mathematical expressions, in this case a and b are inputs, wrapped in Value object with value equal to -4.0 and 2.0, respectively.

2

a and b are transformed to c, d, e and eventually f, g. Mathematical operators are implemented, like +, *, **, even relu().

3

Value object contains data, and grad.

4

Call backpropagation() process.

24.7041
138.8338
645.5773

derivative of a simple function with one input

❓What exactly is derivative❓

import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

A simple quadratic function:

def f(x):
    return 3*x**2 - 4*x + 5

f(3.0)

20.0

Input also can be an array, we can plot it for visibility.

xs = np.arange(-5, 5, 0.25)
ys = f(xs)
plt.plot(xs, ys)

If we bump up a litle value h of x, how f(x) will response?

h = 0.000000000001
x = 3.0
( f(x+h) - f(x) ) / h

1

Change the value of h from 0.0001 to be 0.00000...0001 -> the slope value comes to 14 (at the value of 3.0 of x).

14.001244608152774

Try for x = -3.0, x = 5.0, we get different values of the slope, for x = 2/3, the slope is zero. Let’s get more complex.

derivative of a function with multiple inputs

a = 2.0
b = -3.0
c = 10.0
d = a*b + c
print(d)

4.0

Put our bump-up element to this multi-variables function:

h = 0.001

# input
a = 2.0
b = -3.0
c = 10.0

d1 = a*b + c
a += h
d2 = a*b + c

print('d1: ', d1)
print('d2: ', d2)
print('slope: ', (d2 - d1)/h)

1

Do the same for b, c, we’ll get different slopes.

2

We say given b = -3.0 and c = 10.0 are constants, the derivative of d at a = 2.0 is -3.0. The rate of which d will increase if we scale a!

d1:  4.0
d2:  3.997
slope:  -3.0000000000001137

starting the core Value object of micrograd and its visualization

So we now have some intuitive sense of what is derivative is telling you about the function. We now move to the Neural Networks, which would be massive mathematical expressions. We need some data structures that maintain these expressions, we first declare an object Value that holds data.

class Value:
    def __init__(self, data, 
                        _children=(),
                        _op = '',
                        label = ''
                        ): 
        self.data = data
        self.grad = 0.0
        self._backward = lambda: None
        self._prev = set(_children)
        self._op = _op
        self.label =  label

    def __repr__(self) -> str: # a nicer looking for class attributes
        return f"Value(data={self.data})"
    
    def __add__(self, other):
        other = other if isinstance(other, Value) else Value(other) # turn other to Value object before calculation
        out = Value(self.data + other.data, (self, other), '+')

        def _backward():
            self.grad += 1.0 * out.grad
            other.grad += 1.0 * out.grad
        out._backward = _backward

        return out

    def __mul__(self, other):
        other = other if isinstance(other, Value) else Value(other) # turn other to Value object before calculation
        out = Value(self.data * other.data, (self, other), '*')

        def _backward():
            self.grad += other.data * out.grad
            other.grad += self.data * out.grad
        out._backward = _backward

        return out

    def tanh(self):
        x = self.data
        t = (math.exp(2*x) - 1) / (math.exp(2*x) + 1)
        out = Value(t, (self, ), 'tanh')

        def _backward():
            self.grad += (1 - t**2) * out.grad
        out._backward = _backward
        return out

    def backward(self):
        
        # topo order for all children in the graph
        topo = []
        visited = set()
        def build_topo(v):
            if v not in visited:
                visited.add(v)
                for child in v._prev:
                    build_topo(child) 
                topo.append(v)
        build_topo(self)

        # sequentially apply the chain rules
        self.grad = 1.0
        for node in reversed(topo):
            node._backward()

3

the connective tissue of this expression. We want to keep these expression graphs, so we need to know and keep pointers about what values produce what other values. _children is by default a empty tuple.

4

as we added _children, we also need to point out the father - children relationship in method __add__ and __mul__ as well.

5

we want to know the operation between father and child, _op is empty string by default, the value + and - will be added to the operator method respectively.

6

initially assume that node has no impact to the output.

7

this backward function basically do nothing at the initial.

8

implement of backward pass for plus node, += represent the accumulate action (rather than overwrite it), assigne the gradient behaviour for each type of operation, call the _backward concurrently with function.

Setting input and expression:

a = Value(2.0, label='a')
b = Value(-3.0, label='b')
c = Value(10.0, label='c')

a + b

a*b + c

# d = a*b + c rewrite the expression
e = a*b; e.label = 'e'
d = e + c; d.label = 'd'
# d
f = Value(-2.0, label='f')
L = d * f; L.label = 'L'
L

1

which will internally call a.__add__(b)

2

which will internally call (a.__mul__(b)).__add__(c)

Value(data=-8.0)

So that we can know the children:

d._prev

{Value(data=-6.0), Value(data=10.0)}

We can know the operations:

d._op

'+'

Now we know exactly how each value came to be by word expression and from what other values. These will be quite abit larger, so we need a way to nicely visualize these expressions that we’re building out. Below are a-little-scary codes.

import os

# Assuming the Graphviz bin directory path is 'C:/Program Files (x86)/Graphviz2.xx/bin'
os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz/bin' # add with the code, Gemini instructed me this 😪

from graphviz import Digraph

def trace(root):
    # build a set of all nodes and edges in a graph
    nodes, edges = set(), set()
    def build(v):
        if v not in nodes:
            nodes.add(v)
            for child in v._prev:
                edges.add((child, v))
                build(child)
    build(root)

    return nodes, edges

def draw_dot(root):
    dot = Digraph(format='svg', graph_attr={'rankdir': 'LR'}) # LR = from left to right
    nodes, edges = trace(root)
    for n in nodes:
        uid = str(id(n))
        # for any value in the graph, create a rectangular ('record') node for it
        dot.node(name=uid, label="{ %s | data %.4f | grad %.4f}" % (n.label, n.data, n.grad), shape='record') # why is (n.data, ), but not (n.data) ???
        if n._op:
            # if this value is a result of some operations, create an op node for it
            dot.node(name = uid + n._op, label = n._op)
            # and connect the node to it
            dot.edge(uid + n._op, uid)

    for n1, n2 in edges:
        # connect n1 to the op node of n2
        dot.edge(str(id(n1)), str(id(n2)) + n2._op)

    return dot

1

This will collect all nodes to the nodes.

2

This will iteratively recursively collect all nodes to the nodes, add child and node ralationship information to edges.

Remember to let graphviz installed on your machine, not only Python package, I also run this:

import os
os.environ["PATH"] += os.pathsep + 'C:\Program Files (x86)\Graphviz\bin\dot.exe'

Now we can draw 🚀.

draw_dot(d)

So far we’ve build out mathematical expressions using only plus + and times *, all Values are only scalar.

Back to the Value object, we will create 1 more attribute call label, make the expression more complicated by adding intermediate value f, d, out final node will be capital L.

Backpropagation

In backpropagation, we start at the end and are going to reverse and calculate the gradients along all the intermediate values. What we are actually computing for evert single node here is derivative of that node with respect to L.

In neural nets, L represent to a Loss function. And you will be very interested in the derivative of bassically loss function L with respect to the weights of the neural networks.

We need to know how are those leaf nodes a, b, c, f are impacting to the loss function. We call it grad and add this attribute to the Value object.

manual backpropagation example #1: simple expression

draw_dot(L)

Let’s do the backpropagation manually:

1. First we need to calculate the dL/dL, how L will response if we change L a tiny value h. The response simply is 1 so L.grad = 1.0.
2. F = d * f, so dL/dd -> (f((x+h)) - f(x))/h = ((d+h)*f - d*f)/h = h*f/h = f = -2.0. Quite straighforward, so d.grad = -2.0.
3. Similarly, f.grad = d = 4.
   
4. Next, for dL/dc. We first concern dd/dc, we know d = c + e. Same with (2) we will soon know dd/dc = 1.0, by symmetry dd/de = 1.0. Following the Chain Rules \(h'(x) = f'(g(x))g'(x)\), we have dL/dc = dL/dd * dd/dc = -2.0 * 1 = -2.0.
5. By symmetry, dL/de = -2.0.
6. dL/da = dL/de * de/da = -2.0 * b = -2.0 * -3.0 = 6.0.
7. dl/db = dL/de * de/db = -2.0 * a = -2.0 * 2.0 = -4.0.

Chain Rules Wiki

We can also create a function for playing around / gradient check, and not messing up the global scope.

def lol():

    h = 0.0001

    a = Value(2.0, label='a')
    b = Value(-3.0, label='b')
    c = Value(10.0, label='c')
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    f = Value(-2.0, label='f')
    L = d * f; L.label = 'L'
    L1 = L.data

    a = Value(2.0, label='a')
    b = Value(-3.0, label='b')
    c = Value(10.0, label='c')
    c.data += h # dL/dc = -2.0
    e = a*b; e.label = 'e'
    d = e + c; d.label = 'd'
    # d.data += h # dL/dd = -2.0
    f = Value(-2.0 # + h # dL/df = 4.0
                , label='f') 
    L = d * f; L.label = 'L'
    L2 = L.data # + h # dL/dL = 1.0

    print((L2 - L1) / h)

lol()

-1.9999999999953388

So that is backpropagation ~ just recursively applying the Chain Rules, multiplying local derivatives.

preview of a single optimization step

We can change the input that we can control a, b, c, f to see 1 step of the optimization of process.

a.grad = 6.0
b.grad = -4.0
c.grad = -2.0
f.grad = 4.0

a.data += 0.01 * a.grad
b.data += 0.01 * b.grad
c.data += 0.01 * c.grad
f.data += 0.01 * f.grad

e = a * b; e.grad = -2.0; e.label = 'e'
d = e + c; d.grad = -2.0; d.label = 'd'
L = d * f

print(L.data)

-7.286496

We can see the changes, L increased a little bit as expected.

draw_dot(L)

manual backpropagation example #2: a neuron

Anatomy of neurons, we have:

• axon as input \(x_0\);
• synapse string as weight \(w_0\);
• information flows into the cell body will be \(x_0w_0\);
• there are multiple inputs \(x_iw_i\) flow into the cell body;
• the cell body has some bias itself \(b\);
• the cell body processes all information, the output will flow through an activation function ~ which is some kind of a squashing function, like sigmoid, tanh or something like that;

Neural net Structure with an Activation Function, CS231n Stanford 2017

🚀How does the tanh look like? this hyperbolic function will squash the output to the edge values: -1.0 or 1.0.

plt.plot(np.arange(-5, 5, 0.2), np.tanh(np.arange(-5, 5, 0.2))); plt.grid()

We first implement tanh function to our class Value.

def tanh(self):
    x = self.data
    t = (math.exp(2*x) - 1) / (math.exp(2*x) + 1)
    out = Value(t, (self, ), 'tanh')
    return out

Value.tanh = tanh

Let’s take a simple example of 2-dimensional neuron with 2 inputs x1 and x2:

# input x1, x2
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')
# weights w1,w2
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')
# bias of neuron b
b = Value(6.88137358, label='b')
# x1*w1 + x2*w2 + b
x1w1 = x1*w1; x1w1.label = 'x1w1'
x2w2 = x2*w2; x2w2.label = 'x2w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2'
n = x1w1x2w2 + b; n.label = 'n'

o = n.tanh(); o.label = 'o' # not define yet

draw_dot(o)

o.grad = 1.0
n.grad = 1.0 - o.data ** 2
b.grad = n.grad
x1w1x2w2.grad = n.grad
x1w1.grad = x1w1x2w2.grad
x2w2.grad = x1w1x2w2.grad
x1.grad = w1.data * x1w1.grad
w1.grad = x1.data * x1w1.grad
x2.grad = w2.data * x2w2.grad
w2.grad = x2.data * x2w2.grad

From here we will manually calculate the gradient again:

1. do/do = 1, that’s the base case, so o.grad = 1.0.
2. o = tanh(n), follow that Wiki link (and of course can be easily proof) we have do/dn = 1 - tanh(x)^2 = 1 - o^2.
3. n = x1w1x2w2 + b, this is plus node, which gradient will flow to children equally, do/db = do/dn * dn/db = do/dn * 1.
4. By symmertry, do/dx1w1x2w2 = do/db.
5. do/dx1w1 = do/dx1w1x2w2.
6. do/dx2w2 = do/dx1w1x2w2.
7. do/dx1 = w1 * do/dx1w1.
8. do/dw1 = x1 * do/dx1w1.
9. do/dx2 = w2 * do/dx2w2.
10. do/dw2 = x2 * do/dx2w2.

draw_dot(o)

implementing the backward function for each operation

Doing the backpropagation manually is obviously ridiculous and we are now to put an end to this suffering. We will see how we can implement backward pass a bit more automatically.

We create _backward operation for each operator, implement the Chain Rules. Activate the _backward call along with funtion execution.

o.grad = 1.0

o._backward()
n._backward()
b._backward()
x1w1x2w2._backward()
x1w1._backward()
x2w2._backward()

draw_dot(o)

We still need to call the _backward node by node. Now we move to the next step, to implement backward function to whole expression graph.

implementing the backward function for a whole expression graph

In short, we need to do everything after each node before we call the backward function itself. For every node, all dependencies, everything that it depends on has to propagate to it before we can continue backpropagation.

This ordering of graph can be archived using something like topological sort.

Topological Sort, photo credit to Claire Lee

# we first reset the Values
x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')
b = Value(6.88137358, label='b')
x1w1 = x1*w1; x1w1.label = 'x1w1'
x2w2 = x2*w2; x2w2.label = 'x2w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2'
n = x1w1x2w2 + b; n.label = 'n'
o = n.tanh(); o.label = 'o'

Below is the code:

topo = []
visited = set()

def build_topo(v):
    if v not in visited:
        visited.add(v)
        for child in v._prev:
            build_topo(child) # recursively look up all children for v
        topo.append(v)

build_topo(o)
topo

[Value(data=6.88137358),
 Value(data=2.0),
 Value(data=-3.0),
 Value(data=-6.0),
 Value(data=0.0),
 Value(data=1.0),
 Value(data=0.0),
 Value(data=-6.0),
 Value(data=0.88137358),
 Value(data=0.707106777676776)]

We implement the topological sort to backward() (without underscore) function. Now we can trigger the whole process:

o.backward()

draw_dot(o)

fixing a backprop bug when one node is used multiple times ⛔

This a.grad should be 2.0.

a = Value(3.0, label='a')
b = a + a; b.label = 'b' # this case self and other are both a, we should not overwrite the gradient, we should accumulate it.
b.backward()
draw_dot(b)

breaking up a tanh, exercising with more operations

Sometime we do operations between Value and other, like int. We can not do this unless we add below code to __add__ and __mul__ operations. Now we can Value(1.0) + 1.0, or Value(2.0) * 2.

other = other if isinstance(other, Value) else Value(other)

But for 2 * Value(2.0), which will internally call 2.__mul__(Value(2.0)), will not work. We add __rmul__:

def __rmul__(self, other): # other * self
    return self * other

Value.__rmul__ = __rmul__

For exponential, we add epx:

def exp(self):
    x = self.data
    out = Value(math.exp(x), (self, ), 'exp')

    def _backward():
        self.grad += out.data * out.grad
    out._backward = _backward

    return out

Value.exp = exp

For division, we add __truediv__:

def __truediv__(self, other): # self / other
    return self * other**(-1)

Value.__truediv__ = __truediv__

For power, we add __pow__:

def __pow__(self, other): # self ** other
    assert isinstance(other, (int, float)), "TypeError: only supporting int/float power for now"
    out = Value(self.data**other, (self, ), f'**{other}')

    def _backward():
        self.grad += other * ( self.data ** (other - 1)) * out.grad
    out._backward = _backward

    return out

Value.__pow__ = __pow__ 

For subtract, we add __neg__ and __sub__:

def __neg__(self): # - self
    return - self

Value.__neg__ = __neg__ # self - other

def __sub__(self, other):
    return self + (-other)

Value.__sub__ = __sub__

Now we are ready to try tanh in a different way:

x1 = Value(2.0, label='x1')
x2 = Value(0.0, label='x2')
w1 = Value(-3.0, label='w1')
w2 = Value(1.0, label='w2')
b = Value(6.88137358, label='b')
x1w1 = x1*w1; x1w1.label = 'x1w1'
x2w2 = x2*w2; x2w2.label = 'x2w2'
x1w1x2w2 = x1w1 + x2w2; x1w1x2w2.label = 'x1w1 + x2w2'
n = x1w1x2w2 + b; n.label = 'n'

e = (2*n).exp(); e.label = 'e'
o = (e - 1)/(e + 1)
o.label = 'o'
o.backward()

draw_dot(o)

PyTorch comparison

doing the same thing but in PyTorch: comparison

import torch

x1 = torch.tensor([2.0]).double(); x1.requires_grad = True
x2 = torch.tensor([0.0]).double(); x2.requires_grad = True
w1 = torch.tensor([-3.0]).double(); w1.requires_grad = True
w2 = torch.tensor([1.0]).double(); w2.requires_grad = True
b = torch.tensor([6.8813735870195432]).double(); b.requires_grad = True

n = x1*w1 + x2*w2 + b
o = torch.tanh(n)

print(o.data.item())
o.backward()

print('------------------')
print('x1', x1.grad.item())
print('w1', w1.grad.item())
print('x2', x2.grad.item())
print('w2', w2.grad.item())
print('------------------')

0.7071066904050358
------------------
x1 -1.5000003851533106
w1 1.0000002567688737
x2 0.5000001283844369
w2 0.0
------------------

Building the library

building out a neural net library (multi-layer perceptron) in micrograd

We are going to build out a two-layer perceptron.

A 3-layer neural network with three inputs, two hidden layers of 4 neurons each and one output layer. Notice that in both cases there are connections (synapses) between neurons across layers, but not within a layer, photo credit to cs231n

class Neuron:

    def __init__(self, nin):
        self.w = [Value(np.random.uniform(-1,1)) for _ in range(nin)]
        self.b = Value(np.random.uniform(-1,1))
    
    def __call__(self, x):
        activation = sum((wi*xi for wi, xi in zip(self.w, x)), self.b)
        out = activation.tanh()
        return out

    def parameters(self):
        return self.w + [self.b] # list plus list gives you a list

class Layer:

    def __init__(self, nin, nout):
        self.neurons = [Neuron(nin) for _ in range(nout)]

    def __call__(self, x):
        outs = [n(x) for n in self.neurons]
        return outs[0] if len(outs) == 1 else outs

    def parameters(self):
        return [p for neuron in self.neurons for p in neuron.parameters()] # list comprehension
        # params = []
        # for neuron in self.neurons:
        #     ps = neuron.parameters()
        #     params.extend(ps)
        # return params

class MLP:

    def __init__(self, nin, nouts):
        sz = [nin] + nouts
        self.layers = [Layer(sz[i], sz[i+1]) for i in range(len(nouts))]

    def __call__(self, x):
        for layer in self.layers:
            x = layer(x)
        return x

    def parameters(self):
        return [p for layer in self.layers for p in layer.parameters()] # for neuron in layer.neurons for neuron.parameters()]

1

Number of input for the Neuron. w is randomly generated for each input, same for b which is the bias that controll “the happiness”.

2

Object as a function: define the forward pass of the Neuron \(\sum\limits_{i=1}^{nin} w_ix_i+b\), then squash the output using tanh.

3

A Layer is a list of Neurons, nout specifies how many Neurons in the Layer. Each neuron has nin inputs ~ nin-D. We just initialize completely independent neurons with this given dimensionality.

4

A MLP is a sequence of Layers, picture above depicts a 3-layers MLP containing 1 input layer and 3 output layers, we say the size is 4. We sequentially create connection from the input layer to the 1st output layer, 1st output layer to 2nd output layer,…

nin = 3
nouts = [2.0, 3.0, -1.0]
[nin] + nouts

[3, 2.0, 3.0, -1.0]

x = [2.0, 3.0]
n = Neuron(2)
l = Layer(2, 3)
n(x)
l(x)

[Value(data=0.6482171154461839),
 Value(data=-0.9819100896618514),
 Value(data=0.42012274248341236)]

x = [2.0, 3.0, -1.0]
m = MLP(3, [4, 4, 1]) # a MLP with 3-D input, 3 output layers contains 4, 4, 1 neurons in each layer respectively
m(x)

Value(data=-0.4705965544324498)

draw_dot(m(x))

creating a tiny dataset, writing the loss function

A simple data set, m() is the MLP we defined above.

xs = [
    [2.0, 3.0, -1.0],
    [3.0, -1.0, 0.5],
    [0.5, 1.0, 1.0],
    [1.0, 1.0, -1.0]
]
ys = [1.0, -1.0, -1.0, 1.0] # designed targets

Writing the loss function.

I was unable to sum a list of Value, found the solution here; Edit: I used Numpy random instead of random

ypred = [m(x) for x in xs]
loss = np.array([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)]).sum()

loss

Value(data=3.7846173239470486)

Backpropagation the loss, some magical here:

loss.backward()

We can look into the gradient of weight of the first neuron of the first layer (input layer)

print('value of 1st neuron in 1st layer: ',m.layers[0].neurons[0].w[0].data)
print('grad of 1st neuron in 1st layer: ',m.layers[0].neurons[0].w[0].grad)

value of 1st neuron in 1st layer:  -0.6357735432605731
grad of 1st neuron in 1st layer:  -4.1814374695537895

draw_dot(loss)

collecting all of the parameters of the neural net

We aim to produce the fitness ypred. xs is the data, the input of problem, we can not change it. ys is the ground true, can not changes as well. What we can change is the “paramters” of each neuron, which is weight w and bias b.

We add in to each class a parameters() function to collect those. Finally we can get all the paramters of the MLP:

len(m.parameters())

41

doing gradient descent optimization manually, training the network

Now we will try to change the paramters to minimize the loss, which means our prediction will be more close to the ground true.

Forward pass, calculate the loss:

ypred = [m(x) for x in xs]
loss = np.array([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)]).sum()
loss

Value(data=3.7846173239470486)

Backward pass, calculate the parameters:

loss.backward()

Update the parameters, change the parameters following opposite direction to reduce the loss:

for p in m.parameters():
    p.data += -0.01 * p.grad # we want the p.data go on opposite direction of the loss

0.01 is the learning rate!

New loss

ypred = [m(x) for x in xs]
loss = np.array([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)]).sum()
loss

Value(data=0.885210729994525)

Yeah the loss decreased. In short, the process is:

%%{init: {'theme':'dark'}}%%
flowchart LR

P1(Updated parameters) -- Forward Pass --> L(Loss)
L(Loss) -- Backward Pass --> P2(Parameters to update) 
P2(Parameters to update)  -- Update Pamameters --> P1(Updated parameters)

Automate the training loop:

Warning

For each process, there remained a subtle bug above that we didn’t flush the grads before backpropagation. Because we did not overwrite the gradients (remember the +=), they kept accumulated. The next action of backward and changing parameters using learning rate and grad (which produce a massive step size) become wrong! We must set the grad to zero before backward pass.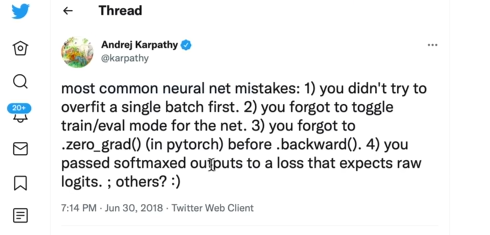

Common guilties when training the NN

for k in range(20):
    # forward pass:
    ypred = [m(x) for x in xs]
    loss = np.array([(yout - ygt)**2 for ygt, yout in zip(ys, ypred)]).sum()

    # backward pass:
    for p in m.parameters():
        p.grad = 0.0
    loss.backward()

    # update params:
    for p in m.parameters():
        p.data += -0.01 * p.grad

    print(k, loss.data)

0 0.885210729994525
1 0.7272070306002337
2 0.6335880961402813
3 0.5694033268577418
4 0.5210728602755308
5 0.48234433619750416
6 0.4499798770914163
7 0.4221446577843293
8 0.3977190488833604
9 0.3759751713337349
10 0.3564130670665513
11 0.33867257920988014
12 0.32248348490480044
13 0.30763598643104695
14 0.29396252735650596
15 0.28132615850080067
16 0.2696128276033427
17 0.25872609733197516
18 0.2485834130081963
19 0.23911338866893608

ypred

[Value(data=0.7723855044989809),
 Value(data=-0.7666895995000865),
 Value(data=-0.7316139699290238),
 Value(data=0.7533418844066474)]

Summary

summary of what we learned, how to go towards modern neural nets

1. What are Neural Nets: they are mathematical expressions, in case of MLP it takes: (1) data as the input, and (2) weights and biases as parameters to build out expression for the forward pass followed by the loss function.
2. The loss function is kind of measure for the accuracy of predictions. The low loss implies that predicted values are matching our targets and the networks are behaving well.
3. The process of Gradient Descent is for each step, we calculate the loss (output of the nets), backwarding it to get paramters, then updating data (which we can change - weights and biases) follow the opposite side of the loss (negative grad * learning rate). We’ll get a lower loss, and backwarding again and again. This process will find the local minimum of the loss.

walkthrough of the full code of micrograd on github

Same with which we built today:

• engine: Value
• nn: Neuron, Layer, MLP, and modulize the zero grad process to class Module
• test: sanity check - compare the backward with torch, also for the forward pass
• demo: a bit complicated example with sklearn dataset, using batch processing when the dataset come large, the loss is slightly different - SVM max-margin loss and using of auto L2 regularization
• learning rate decay: is a scaled as a function of number of iterations, high at begin and low at the end

real stuff: diving into PyTorch, finding their backward pass for tanh

These libraries unfortunately grow in size and entropy, if you just search for tanh it’ll give you thousands of results.

conclusion

There will be follow up session yeah haha.

outtakes :)

Pytorch self-defined autograd.

🤙🚀🔥